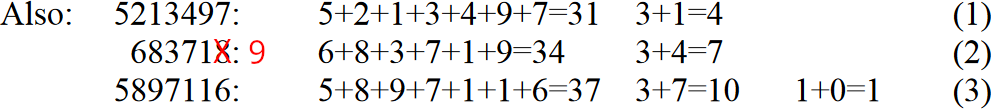|
Der sog. Rechenrahmen mit 10 × 10 Perlen ist dem russischen Abakus (Stschoty) nachempfunden. Während der russische Abakus jedoch für alltägliche Rechnungen im Stellenwertsystem tatsächlich verwendet wurde/wird, benutzt man den Rechenrahmen bei uns i.Allg. nur zur Veranschaulichung in Klasse 1 und 2 der Grundschule im Zahlbereich bis 100 und insbesondere nicht im Sinne eines Stellenwertsystems. |

|
Vertiefungsaufgabe:
Die Subtraktion zweier Zahlen im Zehnersystem kann fast gänzlich durch eine Addition berechnet werden. Dazu bildet man zunächst das sog. Komplement des Subtrahenden und addiert es zum Minuenden. Dabei ist das Komplement einer n-stellige Zahl a der Unterschied zur ebenfalls n-stelligen Zahl 999…9.
Beispiel: Das Komplement von 87 ist 12 (= 99 − 87). Zur Berechnung von 235 − 87 (=148) addiert man zunächst 235 und 12 (=247); und von diesem Zwischenergebnis subtrahiert man 100 und addiert 1:
235 − 87 = (235 + 12) − 100 + 1Allgemein: Ist a eine n-stellige Zahl und C(a) ihr Komplement, dann gilt
b − a = (b + C(a)) − 10n + 1.Begründen Sie diese Rechenstrategie.
Das Ergänzen ist eine Form des Addierens, bei der zwar nur einer der beiden Summanden gegeben ist aber dafür auch die Summe. Bsp: 178 + _____ = 295. Eingestellt wird am Abakus 178; die Zielzahl 295 legen wir mit Ziffernkärtchen darüber. Dann beginnen wir zu addieren: |
178 + _____ = 295 |
Es ist schon paradox, dass die Anzahl der Einer (8) durch Hinzufügen kleiner (5) werden soll. Herkömmlich löst man dieses Problem z.B. durch Auffüllen der Einer auf zehn und anschließendes Bündeln – wie in den Videoclips gezeigt. |
| Hier werden die gewünschten 5 Einer separiert und was übrig ist durch Auffüllen und Bündeln in einem Schritt beseitigt. |
|
Kleine Vielfache einer Zahl können durch wiederholte Addition berechnet werden:
| Z.B. im 8er-System die Aufgabe | 2 × 407 = ? |
|
| Oder im 6×10er-System die Aufgabe | 3 × 1;47;58 = ? |
|
| (Ziehen Sie mit der Maus über die Aufgabe) | ||
| Übungsaufgabe: | ||
| Berechnen Sie im 16er-System | 4 × 356 = | |
| |
Übungsaufgabe:
Halbieren Sie 1;43;52 (im 6×10er-System).Ergebnis: ½ von 1;43;52 =
Von besonderem Reiz ist das Verdoppeln und Halbieren am Rechenrahmen. Denn speziell an diesem Gerät kommt diesen beiden Rechenoperationen eine gewisse Eigenständigkeit gegenüber anderen Operationen des Vervielfachens und Teilens zu – wie wir gleich sehen werden (s.a. „Wechselspiele“, ![]() ,
, ![]() ).
).
Zum „Weiterforschen“:
Verdoppeln Sie die Zahlen 734 sowie 861 am Rechenrahmen, indem Sie jeweils mit der höchsten Stelle beginnen. ![]() ,
, ![]() .
Fällt Ihnen dabei etwas auf?
.
Fällt Ihnen dabei etwas auf?
Wenn wir z.B. 7 verdoppeln, dann schieben wir letztlich so viele Kugeln zurück in den Vorrat, wie dort schon liegen nämlich 3. Und weil dieses Prinzip allgemein beim Verdoppeln von 5, 6, 7, 8 und 9 gilt, kann man sich viel Kopfrechnen beim Verdoppeln am Rechenrahmen sparen und diese Operation weitestgehend mechanisieren:
Sind weniger als 5 Kugeln an einem Draht eingestellt, dann füge ich genau so viele hinzu. Sind es aber 5 oder mehr, dann nehme ich so viele weg, wie im Vorrat liegen, und füge an der nächst höheren Stelle eine Kugel hinzu.Damit haben wir ein eigenständiges Verfahren zum Verdoppeln von Zahlen am Rechenrahmen oder Stschoty entdeckt – oder wiederentdeckt. Denn es ist wohl anzunehmen, dass frühere Rechenmeister dieses Verfahren kannten.
| |
Betrachten wir uns nun das Halbieren am Rechenrahmen.
![]() Wenn wir die Summe 268+123 (=391) bilden, indem wir zunächst 268 am Abakus legen, dann 123 und anschließend bündeln, dann können wir auch versuchen 123 vom eben erhaltenen Ergebnis 391 wieder wegzunehmen (391–123).
Wenn wir die Summe 268+123 (=391) bilden, indem wir zunächst 268 am Abakus legen, dann 123 und anschließend bündeln, dann können wir auch versuchen 123 vom eben erhaltenen Ergebnis 391 wieder wegzunehmen (391–123).
Übungsaufgabe: Berechnen Sie
Bemerkung zu d): Wie bei der Addition gibt es auch bei der Subtraktion am Rechenrahmen zwei Strategien zur Stellenüberschreitung (hier an der Einerstelle, minus 3).
Vielfache einer beliebigen Zahl n berechnen wir bislang, indem wir n so oft addieren, wie es in der Aufgabenstellung verlangt ist:
Die Möglichkeit, das 10-fache einer Zahl durch die übliche Veränderung an den Ziffern zu bestimmen, ist für Kinder überraschend, weil es entsprechend einfache Regeln für andere Vielfache wie z.B. das 11-fache oder das 9-fache nicht gibt. (Man könnte bei der Multiplikation mit 11 z.B. erwarten, dass eine „1“ angehängt wird.)
![]() Kinder, die das 10-fache von Zahlen anfangs noch durch wiederholten Addition am Schulabakus bestimmen, erkennen recht schnell folgende
Regel zur Verkürzung des Verfahrens:
Kinder, die das 10-fache von Zahlen anfangs noch durch wiederholten Addition am Schulabakus bestimmen, erkennen recht schnell folgende
Regel zur Verkürzung des Verfahrens:
Am Schulabakus erhält man das 10-fache einer Zahl, indem man diese Zahl um eine Stelle nach links verschiebt.
Wie lässt sich die Gültigkeit dieser Regel auf andere Stellenwertsysteme ausweiten? Suchen Sie nach geeigneten Beispielen.
|
102 × 1012 |
108 × 1238 |
Am Schulabakus erhält man in jedem Stellenwertsystem das 10-fache einer Zahl, indem man diese Zahl um eine Stelle nach links verschiebt.
Dabei ist 10 selbst als Zahl dieses Systems anzusehen: 10b (b gibt die Bündelgröße des Systems an).
Mit der Kenntnis des 10-fachen einer Zahl n im Zehnersystem können wir uns weitere Vielfache dieser Zahl erschließen, z.B.
| → | das 11-fache: | 10 × n + n, (Distributiv-Gesetz) |
| → | das 9-fache: | 10 × n − n, (Distributiv-Gesetz) |
| → | das 5-fache: | 10 × n : 2. |
Wie sind diese Rechenstrategien nun auf andere Stellenwertsystem zu übertragen? Betrachten wir dazu die Zahl 123 im 8er-System:
- 11 × 123 = 10 × 123 + 123 (→ Rechnung)
- 7 × 123 = 10 × 123 – 123 (→ Rechnung)
- 4 × 123 = 10 × 123 / 2 (→ Rechnung)
Mit den bisher kennengelernten Rechenverfahren (Addition, Subtraktion, Verdoppeln, Halbieren, Verzehnfachen) kann man eigentlich schon alle schulrelevanten Aufgaben zur Multiplikation natürlicher Zahlen berechnen (wobei wir auch die Kenntnis des 100-fachen, 1000-fachen usw. voraussetzen). Um z.B. 8 × 95 (im Zehnersystem) zu berechnen, könnte ein Schüler jeden der im Folgenden skizzierten Rechenwege verwenden:
| 8 × 95 |
|
| 6 × 457 (im 8er-System) |
|
und damit: | 65 × 457 (im 8er-System) |
|
Oftmals sind solche Rechenwege aber recht langwierig und bringen keine Vorteile gegenüber der wiederholten Addition. Im Gegenteil: Bei Kenntnis des 1×1 lässt sich die wiederholte Addition sogar schneller durchführen. Betrachten wir dazu die Aufgabe 7 × 685 im Zehnersystem.
7 × 685(⇒ Das Gleiche als pdf-Datei) |
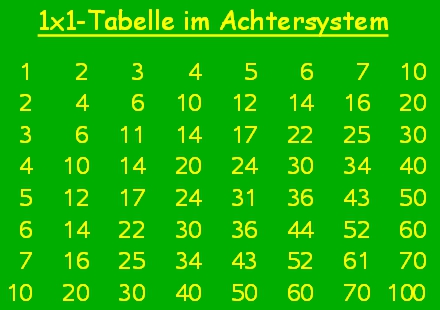
Wollen wir in einem fremden Stellenwertsystem ähnlich effizient rechnen, so müssen wir uns zunächst die entsprechende 1×1-Tabelle bereitstellen. Im 8er-System z.B. sieht sie wie folgt aus:
|
6 × 573 im 8er-System(⇒ Präsentation als pdf-Datei) |
Zur Berechnung eines Produkts mit mehrstelligem Multiplikator, wenden wir die Multiplikation mit 10 (bzw. 100, 1000 usw.) an. Um etwa 648 × 5738 zu berechnen, kommt als neuer Schritt nur die Berechnung von 608 × 5738 hinzu. Der Rest der Aufgabe läuft wie gehabt:
648 × 5738 = 608 × 5738 + 48 × 5738 = 108 × (68 × 5738) + 48 × 5738mit 68 × 5738 = 43428 (siehe oben) und 48 × 5738 = 27548 (selbst nachrechnen!) folgt:
648 × 5738 = 108 × 43428 + 27548 = 434208 + 27548 = 463748
Durch kompaktere Schreibweisen gelangt man von diesen Gedanken ausgehend zu ähnlichen Verfahren wie dem üblichen Schulverfahren (siehe Wechselspiele ![]() ).
).
Nachfolgend ein Vorschlag von uns zur Schreibweise bei fremden Stellenwertsystemen:
648 × 5738 (⇒ Präsentation als pdf-Datei) |
Es geht uns aber auch hier nicht darum, möglichst kompakte und schnell zu notierende Verfahren zu entwickeln. Wir wollen bei allen Rechnungen stets deren Begründung im Auge behalten, was sich ab einem gewissen Grad der Automatisierung nicht mehr gewährleisten lässt.
Zum Öffnen der pdf-Datei bitte hier klicken: → „Rechnen mit Kopf und Händen.“
In einer Tüte Gummibärchen sind 120 Stück drin. Peter isst jeden Tag 13 Stück davon. Wie lange hält die Tüte?Versetzen wir uns in ein Kind der zweiten Klasse, das nicht dividieren oder multiplizieren kann aber immerhin addieren und subtrahieren. Die Idee zur Lösung der Aufgabe besteht darin, auszurechnen wie viele Gummibärchen nach dem ersten Tag noch vorhanden sind, und nach dem zweiten Tag usw.
|
⇒ Peter kann 9-mal 13 Gummibärchen aus der Tüte nehmen und es bleiben dann noch 3 Stück übrig. Die Tüte hält somit 9 Tage.
Das notieren wir so: 120 ÷ 13 = 9 Rest 3 und verwenden das Divisionszeichen mit dem Minus, um unseren Rechenweg anzudeuten. |
Das Divisionszeichen ÷ wurde wohl erstmals von J.C.V. Hoffmann im 19. Jh. vorgeschlagen, um eine Division im Sinne des Aufteilens zu kennzeichnen (Ein wiederholter Vorschlag zur Beseitigung einer bedauerlichen Verwirrung in der niederen Arithmetik betr. das „Dividieren“, Zeitschr. für mathematischen und naturwissenschaftlichen Unterricht, 1891, 22. Jahrg., S. 179-181).
| Aufteilen nennt man einen Vorgang, bei dem von einer gegebenen Menge der Größe a so lange Portionen der Größe b weggenommen werden, bis der Rest r der Menge kleiner ist als b. Man schreibt dann: a = n × b + r oder a ÷ b = n Rest r. |
3 ÷ 2 = 4 ÷ 3 ?
Im Sinne der obigen Definition ist diese Aussage richtig! Denn beide Divisionen ergeben „1 Rest 1“. Wegen des offensichtlichen Widerspruchs zur entsprechenden Bruchgleichung wurde vielfach der Versuch unternommen, die Division mit Rest anders zu schreiben. Das Problem ist jedoch nicht die Schreibweise des Ergebnisses, sondern die Tatsache, dass die Division mit Rest nicht die gleiche Rechenoperation ist wie die Division von rationalen Zahlen (Brüchen). Im ersten Fall besteht das Ergebnis nämlich aus zwei natürlichen Zahlen (Quotient und Rest) und im zweiten aus einer rationalen Zahl (1,5 ≠ 1 Rest 1 ≠ 1,33…). Unterrichtspraktisch kommt der vermeintliche Widerspruch ohnehin nicht vor, da u.E. die meisten Schüler die Division von rationalen Zahlen als eine Präzisierung oder Weiterentwicklung der Division mit Rest auffassen.
Übungsaufgabe:
Berechnen Sie im 8er-System (durch wiederholte Subtraktion): 1008 ÷ 128 = ?
→ Lösung
Zurück zu den Gummibärchen:
Schneller geht die Aufgabe zu lösen, wenn man etwa zwei Portionen auf einmal subtrahiert:
„Zu Anfang sind es 120 Gummibärchen. Nach zwei Tagen sind es noch 120 – 26 = 94 Stück. Nach weiteren zwei Tagen sind es noch 94 – 26 = 68 usw.“Und nichts hindert uns daran, beliebige Vielfache der Portionsgröße zu subtrahieren – sofern wir sie leicht berechnen können:
Solche Rechnungen (120 ÷ 13) können Kinder im zweiten Schuljahr an Abakus/Stellentafel ausführen!
120 – 26 = 94 (2×) 94 – 39 = 55 (3×) 55 – 52 = 3 (4×) 9×
Hinter jeder Subtraktion notieren wir, welches
Vielfache der Portionsgröße subtrahiert wurde,
und erhalten wiederum: 120 ÷ 13 = 9 Rest 3.
Übungsaufgabe:
Berechnen Sie im 8er-System durch wiederholte Subtraktion – aber diesmal unter Verwendung von Vielfachen des Divisors: 1008 ÷ 128 = ?
→ Lösung
Der letzte große Schritt zur Berechnung beliebiger Divisionsaufgaben besteht in der Verwendung des 10-fachen des Divisors (sowie des 100-fachen …). Betrachten wir dazu folgendes Beispiel:
Nach diesem Schema können Schüler alle in der Schule vorkommenden Divisionsaufgaben berechnen und dabei je nach ihren individuellen Rechenfertigkeiten mehr oder minder geschickt vorgehen.
1200 ÷ 13 = ? 1200 – 130 = 1070 (10×) 1070 – 390 = 680 (30×) 680 – 520 = 160 (40×) 160 – 130 = 30 (10×) 30 – 26 = 4 (2×) 92× ⇒ 1200 ÷ 13 = 92 Rest 4
Übungsaufgabe:
Berechnen Sie im 8er-System: 12348 ÷ 148 = ?
→ Lösung
Um zur üblichen Notationsform der Division zu gelangen,
… notiert man zum einen die Subtraktionen untereinander:1200 ÷ 13 = |
… und subtrahiert zum anderen möglichst große Vielfache:
1200 ÷ 13 = |
Eine spezielle Form des Verteilens haben wir mit dem Halbieren schon unabhängig von der Division kennen gelernt. Und die zugrunde liegende Handlungsweise lässt sich natürlich auf andere Divisoren verallgemeinern (dritteln, vierteln, …).
| Verteilen nennt man einen Vorgang, bei dem eine Menge der Größe a in eine vorgegebene Anzahl von n gleichgroßen Portionen und ggf. einen Rest zerlegt wird, der nicht in n Portionen zerlegbar ist. Man schreibt dann: a = n × b + r oder a / n = b Rest r. |
Bemerkung:
Den Schrägstrich / verwenden wir, wenn die Division im Sinne des Verteilens gedacht ist, so wie wir das Zeichen ÷ zur Betonung des Aufteilens verwenden. Mathematisch gesehen besteht kein Unterschied zwischen diesen beiden Versionen der Division und man verwendet deshalb i.Allg. nur ein Zeichen.
Während das Aufteilen in naheliegender Weise verschriftlicht werden kann, ist das beim Verteilen mitunter gar nicht möglich. Versuchen Sie doch 123 / 13 schriftlich zu rechnen: 1 / 13 geht nicht, 12 / 13 geht auch nicht – aber wie dann? Man bedient sich in solchen Fällen des Aufteilens, 123 ÷ 13. Deshalb ist es sinnvoll, im Unterricht das Aufteilen vor dem Verteilen zu behandeln.
Warum führen Aufteilen und Verteilen zum gleichen Ergebnis? Stellen Sie ich vor, Sie verteilen Gummibärchen aus einer großen Tüte an Ihre Schüler. Um die Handlungsweise des Verteilens zu betonen, gehen Sie mit der Tüte reihum und geben jedem Schüler genau eins. Sobald Sie jedem eins gegeben haben, beginnen Sie wieder von vorne. Diesen Vorgang wiederholen Sie so lange, bis nichts mehr übrig ist. Aber oh weh! Mitten in einer solchen Verteilrunde geht Ihnen der Vorrat aus. Ein Teil der Klasse hat schon ein weiteres Gummibärchen erhalten, ein andere Teil aber noch nicht. Eine peinliche Situation ist das. Die bereits verteilten Gummibärchen kann man nicht mehr zurückholen – etliche sind schon verzehrt –, und weitere haben Sie nicht. Das hätte jedoch nicht passieren müssen! Sie brauchen dafür auch nicht die ganze Tüte vorab auszuzählen. Sie hätten nur prüfen müssen, ob für jeden Schüler noch ein Gummibärchen vorhanden ist, ehe Sie eine Verteilrunde starteten.
Indem Sie nun Runde um Runde zuerst eine Portion Gummibärchen – eins pro Schüler – aus der Tüte nehmen, ehe Sie diese verteilen, kommt eine neu Frage auf: Wie viele solche Portionen können Sie aus dem Gesamtvorrat bilden? Es ist bemerkenswert, dass aus dem ursprünglichen Verteilen (a / n, d.h. Zerlegen einer Menge der Größe a in eine vorgegebene Anzahl von n gleichgroßen Portionen) ein Aufteilen geworden ist (a ÷ n, d.h. Zerlegen einer Menge der Größe a in Portionen der Größe n). Und wie viele Portionen sind es? Genau so viele wie jeder Schüler Gummibärchen erhält! Denn von jeder Portion erhält jeder Schüler genau eins.
Sie können die obige Frage auch algebraisch angehen: → hier
Durch Verteilen können wir z.B. die Aufgabe 123 / 3 lösen, indem wir die Zahl 123 am Abakus legen und anschließend daraus drei gleich große Zahlen herstellen.
Übungsaufgabe:
Wie lautet die Lösung von 123 / 3 im 16er-System? Was ist 1;23 / 3 im 6×10er-System?
![]()
![]()
Mit etwas Routine löst man sich schnell von der konkreten Handlung am Abakus – denkt sich diese nur noch – und führt die Rechnung mithilfe schriftlicher Notizen etwa so aus:
7081 / 5(⇒ Präsentation als pdf-Datei) |
Übungsaufgabe:
Berechnen Sie so oder so ähnlich im 16er-System: 708116 / 5
→ Lösung
Um den Schreibaufwand zu reduzieren, notieren wir den Quotienten nur einmal. Also schreiben wir (wieder im Zehnersystem) statt:
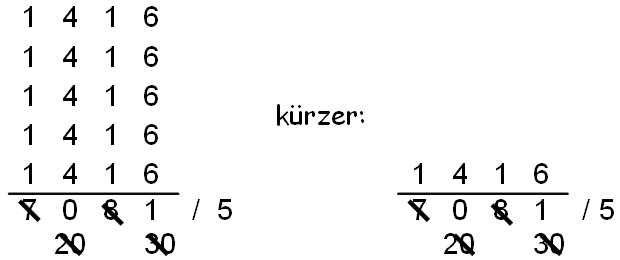
|
| (⇒ Präsentation als pdf-Datei) |
Übungsaufgabe:
Berechnen Sie so oder so ähnlich im gewohnten Zehnersystem: 1234 / 7.
→ Lösung
Obgleich dieses Verfahren durch seine kompakte Notation überzeugt, verlangt es vom Schüler sehr viel Kopfarbeit. Wir wollen uns deshalb eine Variante überlegen, die den Kopf ein wenig entlastet.
1234 / 7(⇒ Präsentation als pdf-Datei) |
Das Verteilen am Abakus ermöglicht eine einfache Herstellung von Kommazahlen (Fachausdruck: Systembrüche)! Dazu wird der herkömmliche Schulabakus um einige Felder nach rechts erweitert. Damit man nachher noch weiß, wo das erste Feld war, legt man rechts davon einen Gegenstand als Markierung. Das Video zeigt in diesem Sinne die Rechnung 53 / 4. ![]()
In anderen Stellenwertsystemen ist lediglich die jeweilige Bündelungsregel anders. Die Division z.B. von 1 / 4 läuft wie folgt:
1 / 4 im 6×10er-System(⇒ Präsentation als pdf-Datei) |
Übungsaufgabe:
Berechnen Sie 1 / 4 im 8er-System und im 16er-System.
![]()
![]()
Auch unendliche periodische Kommazahlen (Systembrüche) lassen sich am Schulabakus leicht einführen. Das Video zeigt die Berechnung von 1 / 3 im 8er-System.
![]()
Übungsaufgabe:
Berechnen Sie im 6×10er-System 1 / 7.
Ergebnis: 1 / 7 =
(Ziehen Sie mit der Maus über die Aufgabe)
Zur Berechnung von Aufgaben des Typs 1/n bietet sich in Anlehnung an die Handlungen an der Stellentafel folgende Notation an (hier am Beispiel 1/7 im Zehnersystem):
1/7 = 0 Rest 1
10/7 = 1 Rest 3
30/7 = 4 Rest 2
20/7 = 2 Rest 6
60/7 = 8 Rest 4
40/7 = 5 Rest 5
50/7 = 7 Rest 1
10/7 = ...
⇒ 1/7 = 0,142857…

|
Die Division zweier natürlicher Zahlen führt entweder zu einem endlichen Systembruch oder zu einem unendlichen, der aber periodisch ist.Denn die Reste bei der Division durch n sind kleiner als n. Deshalb kommt nach spätestens n Divisionsschritten im obigen Verfahren ein Rest vor, der schon einmal da war. Ab dann wiederholen sich alle Reste in der gleichen Reihenfolge.
Eine endlicher Systembruch entsteht bei der Division durch eine Zahl n genau dann, wenn die Primteiler von n Teiler der Basis des Stellenwertsystems sind.Ist nämlich n eine solche Zahl (im Zehnersystem z.B. ein Produkt von 2en und 5en), dann lässt sich der Term 1/n immer so erweitern, dass im Nenner eine Potenz von 10 steht, so dass der entsprechende Systembruch endlich ist.
Allgemein: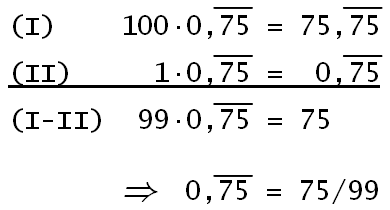
(Im Zehnersystem ist 10n-1 = 999…99 mit n 9en.)
Gilt das Interesse nur der Länge der Periode und nicht den einzelnen Ziffern, dann können wir zu deren Berechnung den eben formulierten Gedanken nutzen: Ist n eine Zahl deren Primteiler keine Teiler der Basis sind, dann ist der Systembruch zu 1/n periodisch und somit das Ergebnis einer Division a/(10k-1), d.h. 1/n = a/(10k-1). Also muss es eine Zahl a geben, sodass n·a = 10k-1 ist – und k ist dann die Länge der Periode. Also muss man eine (kleinste) Zahl k finden, so dass n ein Teiler von 10k-1 ist.
Eine Zahl ist genau dann restlos durch 9 (bzw. 3) teilbar (d.h. sie ist ein Vielfaches von 9 bzw. 3), wenn ihre Quersumme durch 9 (bzw. 3) teilbar ist.
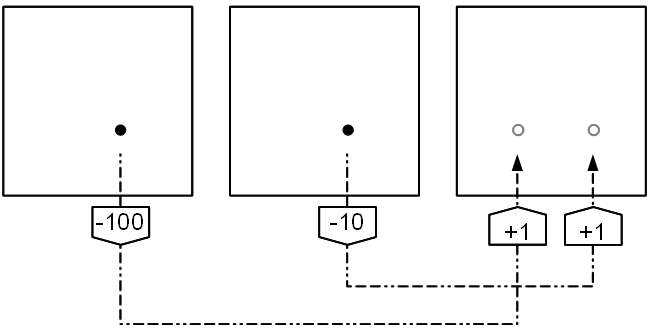 |
Um die Quersumme einer Zahl n zu bilden, die am Abakus liegt, legt man alle Plättchen ins erste Feld. Bezogen auf einzelne Plättchen entspricht dies im Zehnersystem den Rechenoperation –10+1 (= –9), –100+1 (= –99) etc. Also wird bei der Quersummenbildung ein Vielfaches von 9 subtrahiert. Subtrahiert man schließlich auch von dieser Quersumme ein möglichst großes Vielfaches von 9, dann hat man insgesamt nur Vielfache von 9 subtrahiert und was übrig bleibt, ist der Rest der Ausgangszahl n bei Division durch 9. |
Übungsaufgabe:
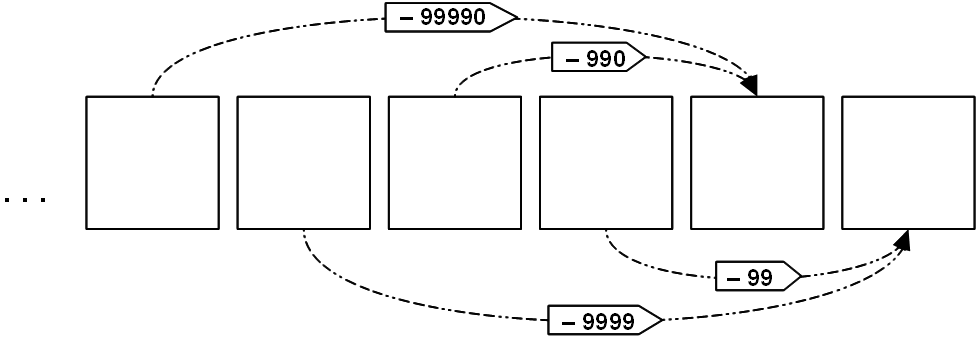 |
Um eine Zahl im Zehnersystem auf Teilbarkeit durch 11 zu testen, bildet man die alternierende Quersumme: Alle Plättchen, an ungeraden Stellen (1. Stelle, 3. Stelle, …) werden ins erste Felde gelegt. Das entspricht den Subtraktionen –99 (= –11·9), –9999 (= –11·909), …. Alle Plättchen an geraden Stellen (2. Stelle, 4. Stelle, …) kommen ins 2. Feld, was den Subtraktionen –990 (= –11·90), –99990 (= –11·9090), … entspricht. Schließlich wird die Differenz zwischen der Anzahl der Plättchen im 1. und im 2. Feld gebildet. Man nimmt also aus dem 1. und 2. Feld gleichviele Plättchen heraus, bis eines dieser beiden Felder leer ist – d.h. man subtrahiert ein möglichst großes Vielfaches von 11. Subtrahiert man schließlich auch von dieser alternierenden Quersumme ein möglichst großes Vielfaches von 11, dann hat man insgesamt nur Vielfache von 11 subtrahiert und was übrig bleibt, ist der Rest der Ausgangszahl n bei Division durch 11. |
Übungsaufgabe:
Formulieren und begründen Sie eine entsprechende alternierende Quersummenregel im 8er-System?
Der Grundgedanke bei der Quersummenbildung findet überraschenderweise eine Anwendung bei folgender Zahlenspielerei (aus: „PIK AS, TU-Dortmund“):
Legt man z.B. die Zahl 34 am Abakus, dann fällt auf, dass es gar nicht nötig ist, alle Plättchen im 1. und 2. Feld zu vertauschen, wie man allein von den Ziffern her meinen könnte (3 ↔ 4). Es genügt hier das Umlegen eines einzigen Plättchens, wie → dieser Grafik zu entnehmen ist. So erklärt sich, weshalb die Differenz zweistelliger Umkehrzahlen eine 9er-Zahl sein muss. Ähnlich lassen sich die Differenzen von → ANNA-Zahlen erklären (z.B. 2112–1221).
Links zu Umkehr/Spiegel-Zahlen und ANNA-Zahlen:
Übungsaufgabe:
Welche Differenzen ergeben ANNA-Zahlen im 16er-System?
Auf der Quersummenregel und der alternierenden Quersummenregel beruhen die → 9er- und 11er-Probe, die dazu dien(t)en, Rechenfehler bei den Grundrechenarten zu erkennen.
Siehe dazu: