Arithmetik - Die natürlichen Zahlen in der Didaktik

Die natürlichen Zahlen im Unterricht

Zahlbilder

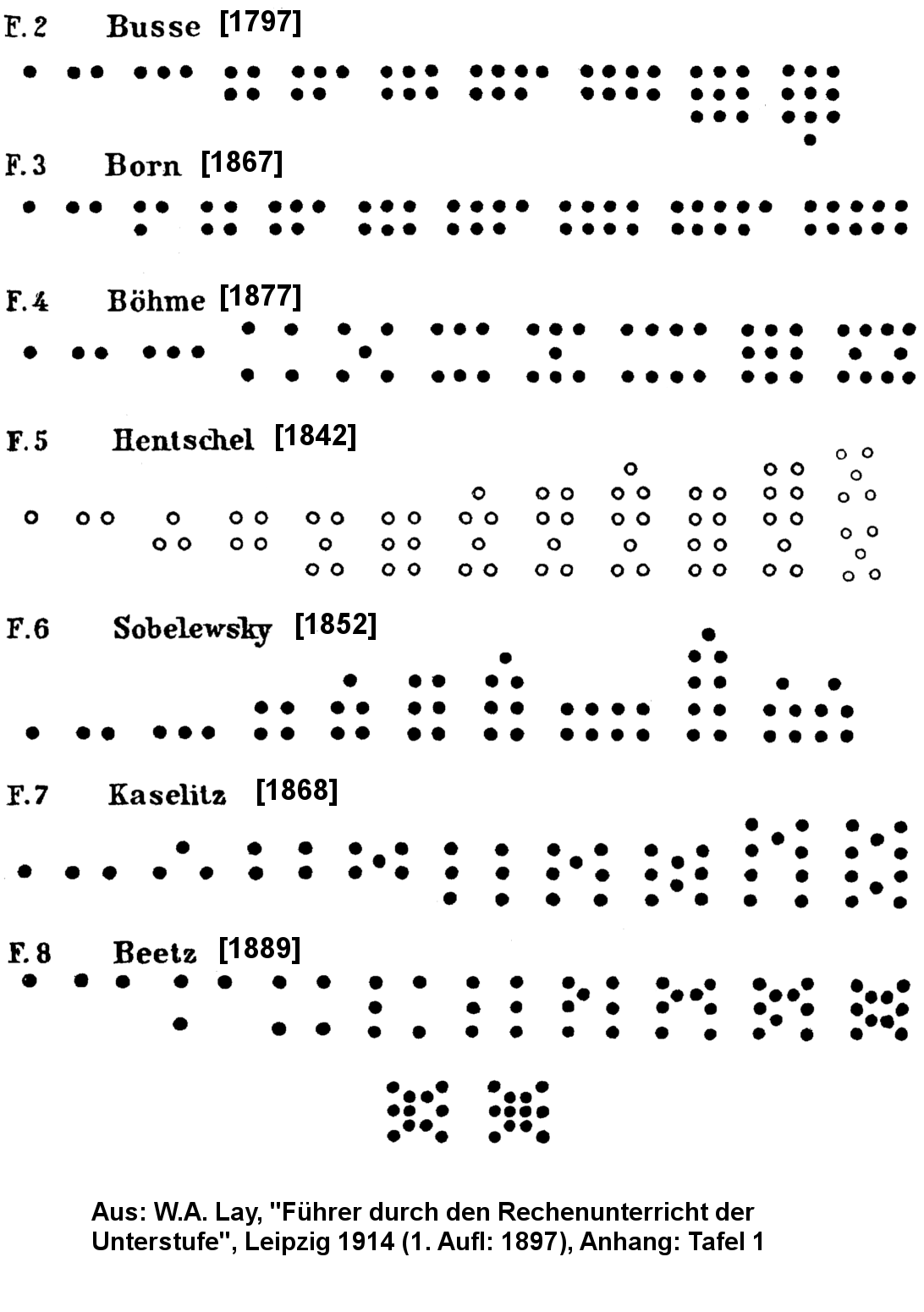
Wir sind in der Lage, kleinere Anzahlen visuell simultan zu erfassen, ohne die einzelnen Objekte zählen zu müssen. Diese Fähigkeit, Subitizing genannt, scheint angeboren zu sein, da nicht nur Erwachsene sondern auch schon kleine Kinder und sogar Tiere sie besitzen. Sobald es aber mehr als vier oder fünf Objekte sind, fällt uns die Erfassung zunehmend schwerer und ab sieben oder acht Objekten können wir das überhaupt nicht mehr ohne Weiteres leisten.

Unter anderem wohl aus diesem Grund bildeten schon Babylonier und Ägypter beim Schreiben ihrer Ziffern einprägsame Muster, wie

Etliche Systeme solch einprägsamer Punktmuster brachte die Zahlbild-Methodik im 19. Jh. hervor, die sie vielfach zur Grundlage des Rechenunterrichts in der Grundschule machte.

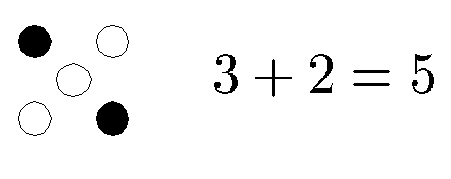
Außer der raschen Erfassbarkeit dieser Punktmuster war für die Zahlbild-Methodik ein wesentlicher Gesichtspunkt, dass man mit ihnen folgendermaßen rechnen konnte: Das Addieren zweier Zahlen sollte als Zusammenfügen zweier Zahlbilder konkret durchführbar sein.

In den Worten des Zahlbild-Methodikers Ernst Hentschel (1804-1875):

„Zahlbilder sind symmetrische, charakteristische Figuren (mathematischen Grundformen entnommen), aus Punkten, Kreisen usw. zusammengestellt, deren Inhalt sich mit einem Blick übersehen läßt, was bekanntlich mit einer Reihe von Strichen, Punkten usw., die mehr als 5 enthält, nicht der Fall ist. Diejenigen Formen der Zahlbilder sind die brauchbarsten, welche bei ihrer Zerlegung in 2 Teile wieder 2 Zahlbilder vors Auge stellen.“ (Zit. nach Kruckenberg, „Die Welt der Zahl im Unterricht“, 1940, S.136)

Möglichkeiten und Grenzen der Methode:

Die Grenzen dieser Methode liegen offensichtlich zum einen in der Schwierigkeit der Darstellung großer Zahlen und zum anderen in der Unmöglichkeit jede mögliche additive Zerlegung einer jeden Zahl (in zwei Summanden) in einem Zahlbild wiederzugeben. Durch welches Zahlbild sollte man etwa die Zahl 27 darstellen? Und wie sollte man z.B. das Zahlbild in und zerlegen?
Der große Vorteil der Zahlbildmethoden ist jedoch, dass sie das Auswendiglernen von Zahlensätzen des kleinen Einspluseins fördern, indem sie als Gedächtnisstütze wirken (s.o. 3+2=5).

Moderne Zahlbildmethoden sind z.B.

die „Kieler Zahlenbilder“ und
das „Würfelhaus-Konzept“.
Das „strategische Fingerrechnen“ ist zwar eigentlich keine Zahlbildmethode, aber es greift wesentlich auf Elemente dieser Methoden zum Aufbau des kleinen Einspluseins zurück: z.B.

5+2=7
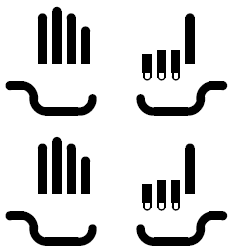7+7=10+4
Gleiches gilt für das Zwanzigerfeld von Wittmann/Müller:

5+2=7

7+7=10+4

Zählzahlen

Das Zählenlernen ist ein Entwicklungsprozess, der i.Allg. zusammen mit dem Sprechenlernen abläuft. Bei Schuleintritt können fast alle Kinder bis zehn zählen und etwa drei viertel aller Schüler bis zwanzig. Nach Gelmann u. Gallistel (1978) genügt das übliche Zählen folgenden fünf Zählprinzipien:

Prinzip der Eins-zu-Eins-Zuordnung:

Jedem der zu zählenden Elemente wird genau ein Zahlwort zugeordnet.

Prinzip der stabilen Ordnung:

Die Reihenfolge der Zahlwörter ist immer die gleiche.

Kardinalzahlprinzip:

Das letzte Zahlwort beim Zählen gibt die Anzahl der gezählten Objekte an.

Abstraktionsprinzip:

Es ist zwar nicht alles abzählbar, aber für alles Abzählbare genügt ein Zählverfahren.

Prinzip von der Irrelevanz der Anordnung:

Die Reihenfolge der Objekte ist beim Zählen beliebig.

Ergänzen könnte man noch das

Prinzip der konventionellen Ordnung:

Die Zahlwörter werden in der üblichen Reihenfolge verwendet.

Kinder vertauschen nämlich durchaus beim Zählenlernen einzelne Zahlwörter und verwenden diese unkonventionelle Reihe stabil über geraume Zeit hinweg. Darüber hinaus eignen sich mitunter auch manche spielerische Abzählreime zum Zählen („enne, denne, fenne, funke, hawe, schnawe, niko, demo, futsch“). Aber all das versteht man herkömmlich nicht unter „zählen“. Andererseits ist die Anzahlbestimmung auch mit einer unkonventionellen Zahlwortreihe denkbar, und das Zählen ist bei Verwendung einer solchen nicht einfach falsch sondern nur unkonventionell.
Ähnliches gilt für das Kardinalzahlprinzip: Es ist nicht falsch, wenn ein Kind für die Anzahl der Striche in „| | |“ die gesamte verwendete Zahlwortreihe „eins, zwei, drei“ wiedergibt, es ist nur unüblich und mit größeren Mengen zunehmend umständlicher, als einfach das letzte Zahlwort anzugeben. Umgekehrt ist es bei Verwendung der Finger zur Anzahlangabe unüblich, nur den letzten Finger zu zeigen (etwa

statt

(!)). Hier werden stets alle zum Zählen verwendeten Finger gezeigt, obwohl wir sie wie die Zahlwörter in einer bestimmten, konventionell festgelegten Reihenfolge verwenden (die übrigens je nach Kultur verschieden sein kann). Will man ein Kind hinsichtlich des konventionellen Kardinalzahlprinzips testen, so ist es also geschickter, eine Menge zu einem Zahlwort herstellen zu lassen und nicht umgekehrt, z.B.: „Gib mir doch bitte fünf Nüsse aus dem Korb.“

Der Prozess des Zählenlernens wurde von Karen Fuson (1988) detailliert untersucht und in die folgenden fünf Stufen untergliedert:

Niveau 1 – String level (ganzheitsauffassung der Zahlwortreihe):

Die Zahlwortreihe wird als Ganzes unstrukturiert eingesetzt, wird wie ein Lied oder ein Gedicht rezitiert: „einszweidreivierfünfsechs“.

Niveau 2 – Unbreakable chain level (unflexible Zahlwortreihe):

Die einzelnen Zahlwörter können klar unterschieden werden, jedoch muss die Reihe immer als Ganzes aufgesagt werden (von 1 an).

Niveau 3 – Breakable chain level (teilweise flexible Zahlwortreihe):

Die Zahlwortreihe kann von einem beliebigen Zahlwort aus aufgesagt werden. Vorgänger und Nachfolger können genannt werden. Rückwärtszählen gelingt zum Teil.

Niveau 4 – Numerable chain level (flexible Zahlwortreihe):

Von jeder Zahl aus kann eine bestimmte Anzahl Schritte weitergezählt werden: Zähle von 14 aus drei Schritte vorwärts.

Niveau 5 – Bidirectional chain level (vollständig reversible Zahlwortreihe):

Es kann von jeder Zahl aus vorwärts und rückwärts gezählt werden.

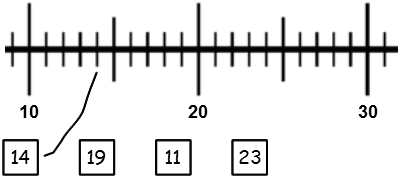
Mit dem Zählen eng verbunden ist die Arbeit am Zahlenstrahl. Eine typische Übung besteht etwa darin, zu einer vorgegebenen Zahl (z.B. 23) den entsprechenden Punkt auf auf einem Ausschnitt des Zahlenstrahls zu lokalisieren.

Dazu geht ein Schüler zu einem bereits bezeichneten Punkt des Strahls (hier: 20) und zählt von dort aus die Skalenstriche weiter, bis er zur genannten Zahl (23) kommt. Genauso wird im umgekehrten Fall bei vorgegebenem Punkt auf dem Strahl die zugehörige Zahl ermittelt, und in ähnlicher Weise laufen andere Übungen zum Rückwärtszählen oder zur Bestimmung von Nachbarzahlen ab. Diese Art der Zahlverwendung am Zahlenstrahl nennt man ordinal: Die Zahlen bezeichnen Stellen in einer linear geordneten Menge.
Andererseits kann man sich fragen, was die Zahlen am Zahlenstrahl zählen? Die Punkte/Skalenstriche sind es jedenfalls nicht! Denn der erste Skalenstrich ist mit 0 bezeichnet. – Eine ähnliche Frage stellt sich in Bezug auf die Skala von Linealen, und dort wissen wir, dass die Zahlen angeben, wie oft eine bestimmte Maßeinheit (z.B. cm) von 0 bis zum jeweiligen Skalenstrich abgetragen werden kann (lückenlos und ohne Überlappung). Also können wir bezüglich des Zahlenstrahls folgern, dass die Zahlen an den Strichen die Anzahl der Intervalle angeben, die zwischen 0 und dem jeweiligen Skalenstrich liegen und so groß sind wie das Einheitsintervall [0;1]. Man nennt diese Art der Zahlverwendung kardinal: Die Zahlen geben eine Anzahl an.

Im ersten Schuljahr verwendet man statt des Zahlenstrahls z.B. eine Zwanzigerreihe:

Die oben beschriebenen Übungen am Zahlenstrahl sind hierauf ebenso anwendbar. Im Unterschied zum Zahlenstrahl fallen an dieser Reihe aber der ordinale und der kardinale Aspekt der Zahlen insofern zusammen, als die jeweilige Zahl nicht nur einen Kreis lokalisiert sondern auch angibt, wie viele Kreise es vom ersten bis zu diesem einschließlich sind.

Die Reihe der gesprochenen Zahlwörter weist im Deutschen (u.a. Sprachen) eine heterogene Struktur auf, die darauf hindeutet, dass ihre Entstehung in unterschiedlichen Phasen und unter verschiedenen Gesichtspunkten verlaufen ist. Diese Struktur unterscheidet sich stark von der der geschriebenen Ziffernzahlen, was schon bei der Zahl 10 auffällt, die wir im Sinne des Stellenwertsystems als „Einsnull“ (oder „Nulleins“) aussprechen müssten.

Die Zahlwörter von 1 bis 19:

Die Zerlegbarkeit in Einer und Zehner ist zwar erkennbar, jedoch erst ab 13 („drei-zehn“) und nicht schon ab 10!

Etymologisch gesehen bedeutet das Wort „zwölf“: zwei bleiben (ahd. zwelef, Zusammensetzung aus zwei und left wie engl. übrig bleiben).
„Elf“ hat die entsprechende Bedeutung: eins bleibt (germanisch aina-lif, einer bleibt).

(Zehn bedeutet übrigens „zwei Hände“.) Konsequenterweise müsste man die Zahlwortreihe nach zwölf weiterführen etwa mit „dreilef, vierlef, fünflef, sechslef, siebenlef, achtlef, neunlef“. Im Litauischen geschieht das: dešimt (10), vienuolika (11), dvylika (12), trylika (13), keturiolika (14) … devyniolika (19), dvidešimt (20).
Im Unterricht der ersten Klasse lässt sich dieser Bruch zwischen 12 und 13 nutzen, um Kindern den Aufbau der Zahlen von 11 bis 19 aus den Einern und einem Zehner bewusst zu machen. Zählt man mit Kindern rückwärts bei 19 beginnend und betont dabei die Einer („neun-zehn“, „acht-zehn“, …), so sind sie mitunter geneigt, nach „drei-zehn“ „zwei-zehn“ zu sagen. In einer anschließenden Diskussion, warum man nicht zweizehn sagt, kann das Bewusstsein für den Aufbau der Zahlen im Stellenwertsystem geweckt werden.

Die Zahlwörter von 20 bis 99:

Ein typisches Zahlwort aus diesem Bereich ist „dreiundvierzig“. Es besteht hörbar aus den Teilwörtern „drei“, „und“, „vier“ sowie „zig“. Man errät leicht, dass zig ursprünglich einmal „Zehner“ bedeutete. Abgesehen von einigen kleineren Lautveränderungen wie bei den 20er Zahlen („zwan-zig statt „zwei-zig) folgt die Bildung der Zahlwörter durchweg der Regel <Einer>und<Zehner>zig bzw. <Zehner>zig, bei reinen Zehner-Zahlen, wobei für <Einer> bzw. <Zehner> das entsprechende Zahlwort einzusetzen ist.
Um den Aufbau der Zahlen bis 99 Kindern der zweiten Klasse bewusst zu machen, kann man diese Systematik der Zahlwortbildung auf die Zahlen von 10 bis 19 anwenden: „neunundeinzig, achtundeinzig, …, zweiundeinzig, einundeinzig, einzig“.

Die Zahlwörter von 100 bis 999:

Ab 100 werden die Zahlwörter so gebildet, dass man mit dem höchsten Stellenwert beginnt: 234, zweihundertvierunddreißig. Das ist genau umgekehrt zu den Zahlen unter 100, wo erst die Einer genannt werden, weshalb Zahlwörter über 100 i.Allg. in dieser gemischten Weise gebildet werden.

Zahlaspekte

Die natürlichen Zahlen werden im Alltag in vielfältiger Weise verwendet: „3 Steine“, „3 km“, „Losnummer 3“, „Seite 3“. Diese Verwendungsweisen bezeichnet man als Zahlaspekte und klassifiziert sie herkömmlich wie folgt:

Kardinalzahlaspekt:

Die Zahl gibt die Anzahl der Elemente einer Menge an, z.B. 3 Äpfel, 20 Kinder, 7 Zwerge.

Ordinalzahlaspekt:

Die Zahl lokalisiert ein Objekt in einem linear Bezugssystem, z.B.: „An der 3. Haltestelle muss ich aussteigen.“
Eine spezielle Form dieses Aspekts ist der

Zählzahlaspekt:: Die Zahl wird als Teil der Zählzahlreihe verwendet, z.B.: „Eins, zwei, drei, …“

Maßzahlaspekt:

Die Zahl gibt zusammen mit der Maßeinheit eine Größe an, z.B.: 5 Meter, 3 Stunden, 4 kg

Operatoraspekt:

Die Zahl gibt die Vielfachheit einer Handlung oder eines Vorgangs an, z.B.: „Dreimal am Tag muss ich die Tablette einnehmen.“

Rechenzahlaspekt:

Algebraischer Aspekt:: Mit den Zahlen wird eine Gesetzmäßigkeit ausgedrückt, z.B.: 3+4=4+3 (Kommutativgesetz).
Algorithmischer Aspekt:: Die Zahlen dienen zum Rechnen, z.B.: 345+289=634

Codierungszahlaspekt:

Die Zahl dient der Identifizierung von Personen, Sachen u.Ä. z.B. Postleitzahlen, Telefonnummern, Steuernummern usw.

Die genannten Zahlaspekte überlagern sich teilweise, lassen sich nicht immer eindeutig zuordnen und erfassen manche Zahlverwendung nicht angemessen.

„Es hat zweimal geblitzt.“ Ist hier „zweimal“ ein Operator oder einfach eine Anzahl also Kardinalzahl?
Ist die Nummer, die ein Fußballspieler trägt, eine Codierungszahl, weil sie zu seiner Identifizierung im Spiel dient? Oder ist sie eine Ordinalzahl, da sie an einer bestimmten Stelle in der Auflistung der Mannschaft steht?
„Luka ist 2 cm größer als Sebastian.“ Hier ist „2“ sicher eine Maßzahl, aber sie gibt weder die Größe von Luka noch von Sebastian an sondern nur den Unterschied zwischen beiden. Sollte man für solche Art der Zahlverwendung nicht einen weiteren Begriff einführen wie z.B. Vergeichszahlaspekt oder Unterschiedszahlaspekt?

Aufgrund dieser Probleme schlagen wir eine alternative Klassifizierung vor (s.a. Matros/Johann, „Ursprung und Wandel des Zahlbewusstseins“, 2006, S.234 ff.). Sie geht aus von der Anzahl (Kardinalzahl) als grundlegendem Aspekt von Zahlen und unterscheidet dann einerseits Zahlverwendungen, bei denen ein Bedeutungswandel stattgefunden hat, und andererseits Zahlverwendungen, bei denen ein Bedeutungsverlust eingetreten ist:

Anzahl
(wie oben Kardinalzahl)

Bedeutungswandel

Weitere Aspekte kommen zum Anzahlaspekt hinzu.

Maßzahl:

3 cm (wie oben)

Ordnungszahl:

„… an der dritten Haltestelle …“ (wie oben)

Unterschiedszahl,

additiv:

„… ist 2 cm größer/kleiner als …“

multiplikativ:

„… ist doppelt so alt wie …“

Bedeutungsverlust

Der eigentliche Anzahlaspekt verblasst, d.h. der Bezug zu einer (anderen) Menge zwecks Anzahlangabe wird unbedeutend.

Systemzahl:

Ziffernfolgen, verstanden als Zahlen in Stellenwertsystemen, z.B. 1011₂ (im 2er-System) oder 345+289=634

Figurierte Zahl

Zahlbilder oder allgemein Punktmuster wie das Hunderterfeld im 2. Schuljahr.

Algebraische Rechenzahl:

z.B. 3+4=4+3 (wie oben)

Die o.g. Codierungszahlen subsumieren wir unter Ordnungszahlen, insofern sie in einer geordneten Liste der Identifizierung eines Objekts dienen. Operatoren sind u.E. Anzahlen.

Über Zahlen und Zeichen

In der Mathematik sind Zeichen wie „5“, „127“ oder „VII“ keine Zahlen sondern Zahldarstellungen. Es sind Zeichen für Zahlen aber eben nicht selbst Zahlen. Diese Auffassung ist durchaus naheliegend, da z.B. die Zeichen „zwei“, „2“ oder „II“ als Objekte betrachtet sehr verschieden sind, aber hinsichtlich ihres Gebrauchs als Zahlen i.W. das Gleiche bedeuten. In der Mathematik gibt es keine unterschiedlichen „Zweien“ sondern nur eine Zahl Zwei. Diese Sichtweise führt konsequenterweise zu der Frage nach der eigentlichen Zahl. Die Mathematik interessiert sich i.Allg. jedoch nicht für einzelne Zahlen sondern für Beziehungen zwischen Zahlen. Sie macht Aussagen wie „Für alle natürlichen Zahlen a, b gilt a+b=b+a“ oder „Jede natürliche Zahl (außer 1) ist vollständig und eindeutig in Primfaktoren zerlegbar.“ Zur Begründung ihres Zahlbegriffs hat die Mathematik um 1900 herum mehrere Konzepte entwickelt, die je nach mathematischem Gebiet zur Anwendung kommen. Zwei prominente Konzepte haben wir im vorhergehenden Kapitel dargestellt, nämlich die Kardinalzahlen und die Dedekind-Peano-Axiome.

Für den Unterricht in der Primarstufe ist diese begriffliche Unterscheidung zwischen Zahlen und Zahldarstellungen jedoch eine große Belastung und u.E. nicht fruchtbar. Deshalb bevorzugen wir in diesem Kontext eine andere Sichtweise. Zwar sehen wir solche Objekte, die die Mathematik Zahldarstellungen nennt, auch als Zeichen für etwas anderes an, aber wir bleiben konkret, indem wir sie in einem ursprünglichen Sinne als Zeichen für eine andere konkrete Menge auffassen – genauer gesagt: als Zeichen für die Existenz der Elemente dieser Menge. Damit folgen wir einer allgemeinen semiotischen Charakterisierung des Zeichenbegriffs (s.a. Matros/Johann, „Ursprung und Wandel des Zahlbewusstseins“, 2006, S.78 ff.):

Ein Zeichen ist etwas, wodurch wir uns etwas anderes in gewisser Hinsicht vergegenwärtigen.

Eine Landkarte ist solch ein typisches Zeichen: Durch sie vergegenwärtigt man sich eine Landschaft, aber eben nicht als Ganzes (wie auch?), sondern nur in gewisser Hinsicht, etwa hinsichtlich der Höhenunterschiede oder hinsichtlich der relativen Lagen von Ortschaften.
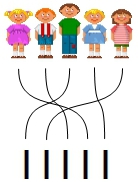
Gelegentlich kommt es vor, dass wir ignorant die Landkarte nicht von der Landschaft unterscheiden. Diese Art der Gleichsetzung von Zeichen und Bezeichnetem ist übrigens Thema des berühmten Bildes La trahison des images („Ceci n’est pas une pipe“) von René Magritte.
(Lesetipp: Wikipedia: Semiotisches Dreieck)

Strichlisten sind ebensolche Zeichen: Durch sie vergegenwärtigt man sich z.B. bei der Klassensprecherwahl die Befürworter der Kandidaten, aber wiederum nicht gänzlich, dazu wäre eine Strichliste nicht brauchbar. Wenn wir das wollten, müssten alle Anhänger der Kandidaten hervortreten. Und das mag wohl die archaische Bedeutung einer solchen Wahl sein: Die Anhänger zweier Kandidaten im Kampf gegeneinander, und Gewinner ist, wer die meisten Anhänger hinter sich vereint. Doch gottlob gibt es Strichlisten, und statt der Personen lassen wir die Striche kämpfen. Dazu notieren wir für jeden Anhänger eines Kandidaten genau einen Strich – der Mathematiker nennt das eine bijektive (oder eineindeutige) Zuordnung. Durch jeden Strich vergegenwärtigen wir uns dann einen Anhänger eines Kandidaten, aber nur in der Hinsicht, dass es ihn gibt, dass er existiert; und jeder andere Strich steht für die Existenz eines anderen, weiteren Anhängers. Schließlich vergleichen wir die Strichlisten der beiden Kandidaten, und Sieger ist, wer mehr Striche hat.

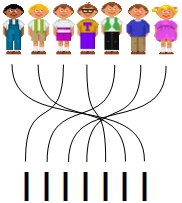Solche Zeichen wie Strichlisten sind die ursprünglichen Anzahlen, wir verwenden dafür den Ausdruck explizite Anzahl:

Eine explizite Anzahl ist eine Menge, durch deren Elemente wir uns alle Elemente eine anderen Mengen hinsichtlich ihrer bloßen Existenz vergegenwärtigen. Dabei steht jedes Element der Anzahl-Menge für die Existenz genau eines Elements der anderen Menge. (Die Mengen sind bijektiv aufeinander abbildbar.)

Unter einer impliziten Anzahl verstehen wir dann weiter ein Zeichen für eine explizite Anzahl, das kürzer ist als diese. Beim Abzählen einer Menge mit Zahlwörtern etwa bilden wir zunächst eine explizite Anzahl („eins, zwei, drei, vier“) und anschließend daraus in umkehrbar eindeutiger Weise eine implizite Anzahl, nämlich das letztgenannte Zahlwort („vier“).

Wie lässt sich nun aber unsere Vielfalt gleichwertiger Anzahlen („zwei“, „2“, „II“, „10₂“ etc.) vereinbaren mit der Einzigkeit der Zahlen in der Mathematik? – Zu einem ähnlichen Problem sagt Aristoteles:

„Die gesprochenen Worte sind die Zeichen von Vorstellungen in der Seele und die geschriebenen Worte sind die Zeichen von gesprochenen Worten. So wie nun die Schriftzeichen nicht bei allen Menschen dieselben sind, so sind auch die Worte nicht bei allen Menschen dieselben; aber die Vorstellungen in der Rede, deren unmittelbare Zeichen die Worte sind, sind bei allen Menschen dieselben und eben so sind die Gegenstände überall dieselben, von welchen diese Vorstellungen die Abbilder sind.“
Aristoteles, Peri hermeneias, Erstes Kapitel (Zit. nach Wikipedia: Semiotik)

Demgemäß fassen wir unterschiedliche Anzahlen als synonyme Wörter aus unterschiedlichen Zahlsprachen auf, sofern sie sich auf die gleiche Menge beziehen (könnten). So sehen wir Strichlisten als eine Zahlsprache und Zahlwörter als eine andere und Systemzahlen als eine abermals andere. Für unseren Alltag ist es wichtig, zwischen unterschiedlichen Zahlsprachen hin und her übersetzen zu können: Von den Zahlwörtern, mit denen wir mündlich kommunizieren, in die dekadischen Systemzahlen, die der schriftlichen Kommunikation dienen, und umgekehrt; manchmal kommen noch römische Zahlen dazu. Im Unterricht werden weitere Sprachen eingeführt: Zahlbilder, Zahlenstrahl, Abakus oder Stellenwerttafel, Bündelmaterial nach Montessori oder Dienes etc. Sie sollen das Erlernen z.B. bestimmter Aspekte des Rechnens erleichtern, weil ihre „Grammatik“ leichter verständlich ist (man denke etwa an Zahlbilder). Aber dafür müssen Kinder schnell von der einen in die andere Sprache übersetzen können; sie müssen sozusagen erst die Vokabeln der Fremdsprache lernen. (Das geht bei Zahlen nicht so wie im Fremdsprachenunterricht.) Für Fremdsprachen gibt es Wörterbücher. Und die nebenstehende Tabelle kann ebenso als Anfang eines Wörterbuchs für die Zahlsprachen darin aufgefasst werden.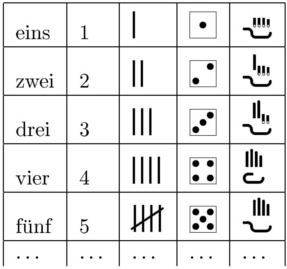

→ Inhaltsverzeichnis